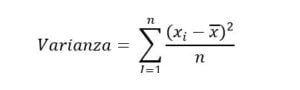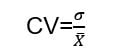El término «varianza» es un concepto estadístico que nos permite comprender de manera más precisa los datos. Además, nos ofrece múltiples enfoques a los que podemos acercarnos.
Desde un punto de vista intuitivo, nos ayuda a entender la idea de dispersión. Desde una perspectiva más formal, tiene diversas aplicaciones en el campo de la estadística. En un mundo en el que los datos gobiernan, es fundamental no pasar por alto esta noción estadística.
En el ámbito empresarial, nos ayuda a comunicarnos de manera más efectiva y a obtener conclusiones útiles de diferentes tipos de informes con mayor facilidad. No poseer conocimientos básicos al respecto se puede considerar una forma de desconocimiento estadístico.
¿Qué es la varianza?
En el contexto de la estadística descriptiva, la varianza puede ser entendida como la media de los valores al cuadrado de las desviaciones respecto a la media. A partir de esta definición, es natural preguntarse por qué calculamos la media de los cuadrados de las desviaciones en lugar de las desviaciones en sí.
La respuesta es simple. Una de las propiedades fundamentales de cualquier media es que la media de las desviaciones respecto a la media siempre es cero. Por lo tanto, utilizamos la varianza.
Vamos a utilizar un ejemplo Supongamos que deseamos calcular la media de los valores 7, 8 y 9. Simplemente tenemos que sumar los valores (que suman 24) y dividir entre 3. Podemos observar que la media es 8. Las desviaciones respecto a la media son -1, 0 y 1. La media de estas desviaciones es 0. Independientemente de los valores que consideremos, el resultado siempre será el mismo.
Elevar al cuadrado las desviaciones antes de calcular la media es una solución para evitar que este cálculo siempre sea cero. Es importante recordar que tanto las desviaciones positivas como las negativas o incluso las nulas, al ser elevadas al cuadrado, nunca son negativas. La suma resultante será mayor o igual a cero. Solo será cero cuando todos los valores sean iguales y, por lo tanto, no haya ninguna desviación respecto a la media.
Sin embargo, al elevar al cuadrado, también elevamos al cuadrado las unidades en las que se mide la varianza. Por ejemplo, si la media se expresa en metros, la varianza se medirá en metros cuadrados. Para evitar este problema, podemos calcular la raíz cuadrada de la varianza, conocida como desviación estándar, que se utiliza en muchas situaciones.
¿Cómo se calcula la varianza?
A través de la siguiente fórmula:
Varianza de una variable aleatoria
Es interesante conocer el cálculo de la varianza de una variable aleatoria, que en su caso se calcularía a través de la siguiente fórmula:
- Var(X) es la varianza de la variable aleatoria discreta X.
- E es la esperanza matemática.
Una variable aleatoria puede ser discreta o continua.
En primer lugar, una variable es aleatoria discreta cuando se toma un número finito o numerable de valores. Por lo tanto, el cálculo sería el siguiente:
En cambio, una variable es aleatoria continua si si toma un número infinito no numerable de valores. Se calcula a través de la siguiente fórmula:
- E(X) es la esperanza matemática de la variable aleatoria X.
- f(x) es la función de densidad de probabilidad de la variable aleatoria X.
¿Qué mide la varianza?
La varianza es una medida de dispersión que busca capturar hasta qué punto los datos se alejan de la media. Si los datos están muy por encima o por debajo de la media, esto se reflejará en una varianza alta.
Imaginemos, por ejemplo, que queremos calcular el salario promedio de dos empresas, cada una con solo dos trabajadores. En la empresa A, los salarios son de 19,500 y 29,500 euros, mientras que en la empresa B son de 16,000 y 33,000 euros. Observamos que en ambos casos, la media es la misma: 24,500 euros. Sin embargo, en la empresa A, los valores están más cercanos a la media en comparación con la empresa B.
En este sencillo ejemplo, no es necesario calcular la varianza para notar de manera rápida que la media es más representativa en la empresa A. Sin embargo, si tuviéramos cientos, miles o millones de datos, sería útil contar con un valor que indique la dispersión.
No obstante, la varianza por sí sola no proporciona información suficiente. En nuestro ejemplo, estamos comparando dos empresas con la misma media, pero necesitamos un valor que nos proporcione un contexto adicional. Después de todo, si las medias son diferentes, es lógico que las varianzas difieran. La solución se encuentra en el coeficiente de variación:
Este coeficiente tiene la ventaja de ser unitario y, por lo tanto, no posee dimensiones. Indica cuántas veces la desviación estándar (raíz cuadrada de la varianza) se encuentra contenida en la media.
Algunas aplicaciones de la varianza
Las aplicaciones estadísticas del concepto de la varianza son numerosas. A continuación, mencionaré algunas de las más destacadas:
- Estimadores eficientes: Son aquellos que tienen una mínima varianza y cuya esperanza coincide con el verdadero valor del parámetro. Esto reduce el riesgo de obtener estimaciones alejadas del valor real del parámetro al extraer información de una muestra.
- Estimadores consistentes: Son aquellos que, a medida que aumenta el tamaño de la muestra, tienden a tener una varianza cercana a cero. Con muestras grandes, la estimación se desvía muy poco del valor real.
- Distribución normal: En esta distribución, la varianza (y su raíz cuadrada, la desviación estándar) es uno de los parámetros clave. A medida que la varianza disminuye, la campana de Gauss se vuelve más alta y estrecha.
- Homocedasticidad en modelos de regresión: Se refiere a la situación en la cual la varianza del error es constante a lo largo de las observaciones. En una regresión simple, por ejemplo, esto se observa cuando los puntos dispersos alrededor de la línea o curva estimada mantienen una dispersión constante.
- Análisis de la varianza (ANOVA): Permite comparar diferentes grupos y analizar los factores que influyen en ellos.
- Desigualdad de Chebyshev: Proporciona límites sobre la probabilidad de que una variable aleatoria se aleje de su esperanza en relación a su desviación estándar (raíz cuadrada de la varianza
La varianza en finanzas
En el ámbito financiero, es común asociar la varianza con el riesgo. En esencia, la varianza refleja la posibilidad de que los resultados difieran significativamente de lo esperado en relación a la varianza. Cuando se comparan dos inversiones con el mismo rendimiento esperado, generalmente se considera más arriesgada aquella que tenga una mayor varianza.
Aplicaciones empresariales
Es evidente que en las múltiples aplicaciones de la estadística en el entorno empresarial, el concepto de varianza resulta relevante. Sin embargo, incluso para aquellos que no son expertos en estadística, existe una perspectiva general que ayuda a comprender los datos.
Por ejemplo, consideremos la visualización de un gráfico. Si observamos una gran dispersión de los datos (alrededor de la media, de una línea de regresión o de cualquier otra representación gráfica), es importante prestar mayor atención y ser cautelosos.
Consideremos unos resultados previos. Es cierto que el hecho de que los resultados anteriores hayan mostrado poca variación con respecto a lo previsto no significa necesariamente que eso se mantendrá en el futuro. Sin embargo, cuando observamos una gran variabilidad, debemos estar más preparados, ya que es más probable que ocurran desviaciones significativas.
En ocasiones, el problema radica en la calidad del análisis estadístico en sí. En otros casos, puede deberse a limitaciones en las metodologías utilizadas o a deficiencias en los datos disponibles. Es posible que el receptor del informe no lo sepa, pero esa dispersión inusual está transmitiendo una señal de advertencia.
Por lo tanto, en última instancia, el concepto de dispersión nos introduce en aspectos como la complejidad y la diversidad. Nos ayuda a analizar los informes de manera crítica y contribuye a evitar conclusiones precipitadas.